- Home
- Dipartimento
- Ricerca
- Didattica
- Post Lauream
- Trasferimento della conoscenza
- Come fare per
Modelli fortemente correlati su reticolo
La materia condensata moderna si occupa di situazioni in cui la fisica quantistica e le interazioni a molti corpi svolgono un ruolo chiave per creare nuovi fenomeni fisici. Per la maggior parte del secolo scorso, la fisica della materia condensata a bassa temperatura è stata dominata dal paradigma della rottura spontanea di simmetria (Landau): alle basse temperature, la materia si riorganizza in fasi ordinate a lungo raggio rompendo una simmetria dell'Hamiltoniana microscopica, testimoniata da parametri di ordine locali. Vi è ormai una chiara evidenza che diversi sistemi possono andare oltre questa descrizione standard, ospitando fasi a bassa temperatura caratterizzate da proprietà topologiche non banali, o eccitazioni di quasiparticelle non convenzionali, che portano solo una frazione dei gradi di libertà originali. Tali fasi topologiche sono robuste rispetto alle perturbazioni, poiché sono legate alla presenza di entaglement immagazzinati nell'intero sistema. Gli esempi includono isolanti Mott, liquidi di spin e fasi topologiche.
I miei sforzi attuali sono dedicati all'identificazione di fasi spin-liquido con eccitazioni gapless o degenerazione topologica negli isolanti di Mott con frustrazione magnetica. Sono anche interessato alle fasi superconduttrici che emergono da forti correlazioni elettrone-elettrone negli orbitali d. L'esempio paradigmatico è dato dalla superconduttività ad alta temperatura nei materiali di ossido di rame. A questo proposito, le fluttuazioni orbitali possono anche portare a fasi non convenzionali, con proprietà sia topologiche che superconduttive che sono lontane dall'essere completamente comprese.
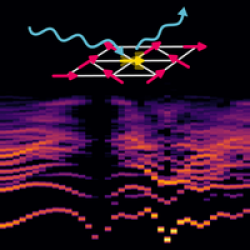
Utilizzando tecniche numeriche (principalmente Monte Carlo quantistico e diagonalizzazioni esatte), indago le proprietà dello stato fondamentale e della bassa energia dei modelli di Hubbard e Heisenberg (inclusi casi multiorbitali o multi-sapore) sul reticolo. I calcoli sono rilevanti per un certo numero di materiali con proprietà non convenzionali a bassa temperatura. La mia recente attività (con L. Viteritti) è anche focalizzata a comprendere come gli approcci di apprendimento automatico possono essere utilizzati per descrivere le funzioni d'onda a molti corpi in modelli di spin frustrati in dimensioni spaziali ridotte.
Info
Ultimo aggiornamento: 11-09-2025 - 08:37