- Home
- Dipartimento
- Ricerca
- Didattica
- Post Lauream
- Trasferimento della conoscenza
- Come fare per
Teoria e Simulazione di Materiali Quantistici
Le proprietà e l'esistenza stessa di tutti i materiali possono essere comprese grazie alle leggi fondamentali della meccanica quantistica, tuttavia esiste una certa classe di sistemi che sono stati progressivamente raggruppati sotto il nome di "materiali quantistici". Con questa dicitura si intendono una varietà di materiali e fenomeni piuttosto eterogenei, che vanno dai superconduttori ad alta temperatura ai sistemi fortemente correlati, agli isolanti topologici, ai materiali di Dirac e al vasto panorama rappresentato dai materiali van der Waals.
Ciò che accomuna tutti i cosiddetti materiali quantistici è la presenza di fenomeni emergenti responsabili del loro comportamento piuttosto esotico, ponendo affascinanti questioni scientifiche legate alle fondamenta della fisica della materia condensata e della scienza dei materiali, un esempio è dato dall'esistenza di quasiparticelle ed eccitazioni emergenti come i fermioni di Dirac, di Weyl e di Majorana.
Il progresso scientifico nel campo dei materiali quantistici è inoltre uno dei fattori chiave nello sviluppo di tecnologie potenzialmente dirompenti, come il calcolo quantistico. Uno scenario importante è rappresentato dalla proposta di utilizzare gli isolanti topologici bidimensionali (2D) come piattaforma per l'elettronica a bassa dissipazione. In questi materiali, mentre tutta la regione interna rimane sempre isolante, i bordi del sistema sono sempre metallici e possono ospitare, in maniera robusta, un trasporto elettronico a bassa dissipazione. Ciò avviene anche in presenza di disordine piuttosto forte (dovuto ad esempio a impurità o difetti), in quanto il fenomeno è “protetto” dalla topologia non banale della funzione d'onda elettronica. Inoltre, si può accendere e spegnere il trasporto di carica e di spin sui bordi di un isolante topologico attraverso un campo elettrico esterno, o tramite la ferroelettricità, un aspetto molto promettente per applicazioni di spintronica.
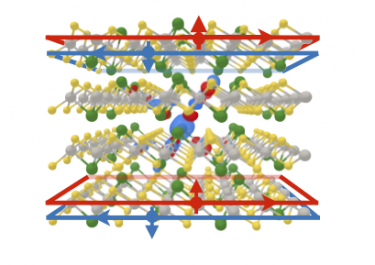
Funzioni di Wannier massimamente localizzate nella jacutingaite (Pt2HgSe3), un isolante topologico duale in cui un invariante Z2 "weak" coesiste con un mirror Chern number. Le frecce blu e rosse rappresentano gli stati di bordo elicoidali, protetti dalla topologia, che scorrono attorno al campione.
In questa linea di ricerca, sfruttiamo tecniche all'avanguardia di simulazione della strutture elettronica ai fini di comprendere, e possibilmente scoprire, nuovi materiali quantistici di interesse per la spintronica e per il calcolo quantistico topologico, focalizzandoci in particolare sugli isolanti topologici e sui materiali 2D. Le tecniche utilizzate spaziano dalla teoria del funzionale densità e dalla teoria delle perturbazioni a molti corpi (GW), alle funzioni di Wannier, alla dinamica molecolare ab initio e al machine learning, tutti supportati da un uso massiccio di infrastrutture di calcolo ad alte prestazioni (HPC). Oltre a complessi studi da principi primi, sviluppiamo nuove teorie e metodi per indagare aspetti geometrici delle struttura elettronica, come gli invarianti topologici.
Info
Ultimo aggiornamento: 08-04-2024 - 20:50