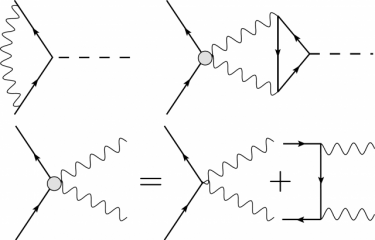
Our research focusses on several interrelated aspects of the QFT framework, such as:
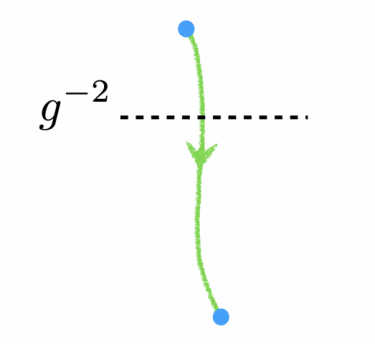
Conformal gauge theories: strongly-coupled gauge theories in various spacetime dimensions d can admit a renormalization group flow connecting them to an interacting conformal field theory (CFT). Gauge theories typically come in families parametrized by the number of colors, the number of matter flavors, and possibly additional parameters such as Chern-Simons couplings. It is not known for what values of these parameters the CFT phase of the gauge theory exists. In d=3 these conformal gauge theories have application to certain second order transitions with persistent order. In d=5 they are the most promising candidate to provide examples of interacting CFTs without supersymmetry, yet unknown. We investigate this problem using resummations of the perturbative expansion, and the epsilon-expansion to approach gauge theories in d=3 and d=5 spacetime dimensions.
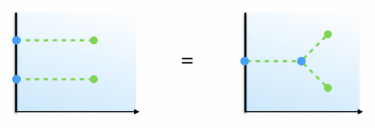
Boundary conditions: studying QFT in spaces with boundaries defines a large set of new observables, the boundary correlation functions for a given boundary condition. Boundary conditions can preserve some symmetry of the bulk theory, such as conformal symmetry, in which case they can be used to describe surface transitions in statistical physics, or supersymmetry. Given a certain QFT, it is an open problem to classify the possible boundary conditions that preserve certain symmetries. We study this problem for simple bulk CFTs, such as free massless fields, and for supersymmetric theories where some observables can be computed exactly.
Quantum field theory in curved space: placing a QFT in a curved background can be used to regulate the infrared behavior and have more control on the dynamics. A particularly nice example is that of the Euclidean Anti-De Sitter (EAdS) space, which in many aspects behaves like a finite-size box, but on the other hand retains a large spacetime symmetry and allows to define asymptotic observables akin to scattering amplitudes in flat space, thanks to the presence of a boundary. We study aspects of QFT in EAdS, going beyond the perturbative regime via large N and boundary CFT techniques. We also use QFT in EAdS as a tool to compute late-time correlators in De Sitter (dS) space, which describes a maximally symmetric expanding universe, having in mind applications to inflationary correlators.